特徴量選択(feature selection)= 「どれを説明変数として使うか」は、データ分析では重要です。このBlogでは、特徴量選択についてXGBoostのアルゴリズムでSPSS® Modeler の特徴量選択とPython Scikit-Learnの結果を比較してみたいと思います。
特徴量選択は、実際のところドメイン知識が大きな力を発揮するため、データサイエンスに精通しないがドメイン知識をもつ専門家にもっと、モデルを作成してもらうためIBM のSPSS® Modeler等の統計ソフトを大手企業、官公庁向の研究者やテータ分析担当者向けに導入が進んでいます。
SPSS® Modeler には、Python 固有のアルゴリズムを使用するためのノードが用意されています。XGBoost Tree© は、 ツリー モデルを基本モデルとして使用する勾配ブースティング・アルゴリズムを実装しており、Python で実装されています。
前提PC環境
この記事で扱うPC環境は以下のとおりです。
| ソフトウエア | バージョン |
|---|---|
| SPSS Modeler | 18.3 on Windows 10 |
| XGBoost on Scikit-learn | 1.4.0 on Python 3.8 |
使うデータはカリフォルニア住宅価格です。Scikit-Learnの標準データセットです。
20640 rows × 9 columns のサイズです。各々のカラムの意味は以下のとおりです。
目的変数はカリフォルニア地区の住宅価格で単位は10万ドルです。データセット自体は1990年の米国国勢調査(U.S. census) のもので、一行に国勢調査で使われるブロックグループ単位で集計されています。ブロックグループは米国国勢調査において、最小の地理的な単位です。概ね、600~3,000人を一つのグループにしています。
世帯(household) は一つの住宅に居住する人数です。平均部屋数、ベッドルーム数はこの統計が世帯当たりで計算していますが、しばしばブロックグループ単位で計算すると「数世帯」と「多くの空き家」があるようなリゾート地では現実離れした大きな数字になる場合があります。それら大きな数字は外れ値としての処理が必要です。
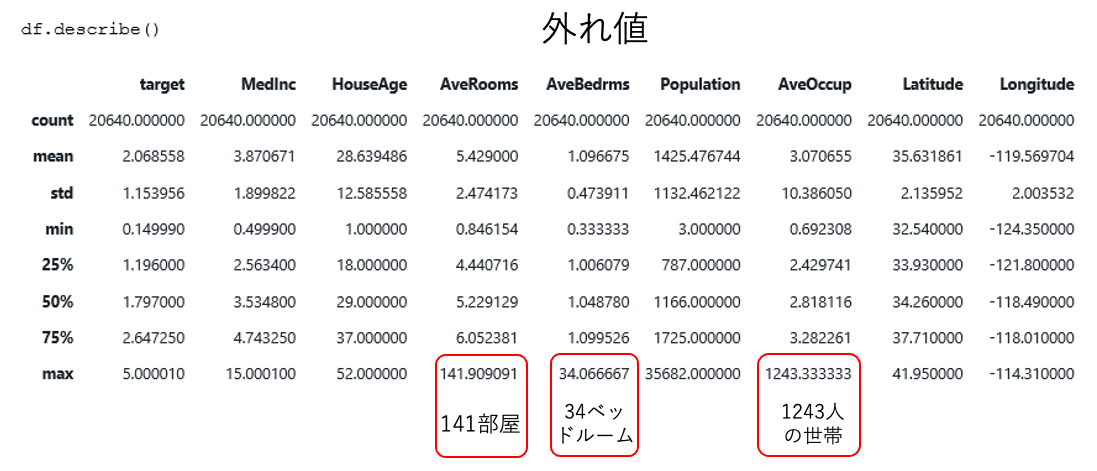
外れ値の求め方には色々な方法があります。代表的な方法は以下の二つです。 いずれも、SPSS Modeler でサポートされています。
- 平均から標準偏差のn倍(例:3倍)を範囲外とする
- 全体のnパーセンタイル(例:0.99)を超えるものを範囲外とする
ここでは、方法2の 99パーセンタイルで平準化した場合の分布イメージを載せます。
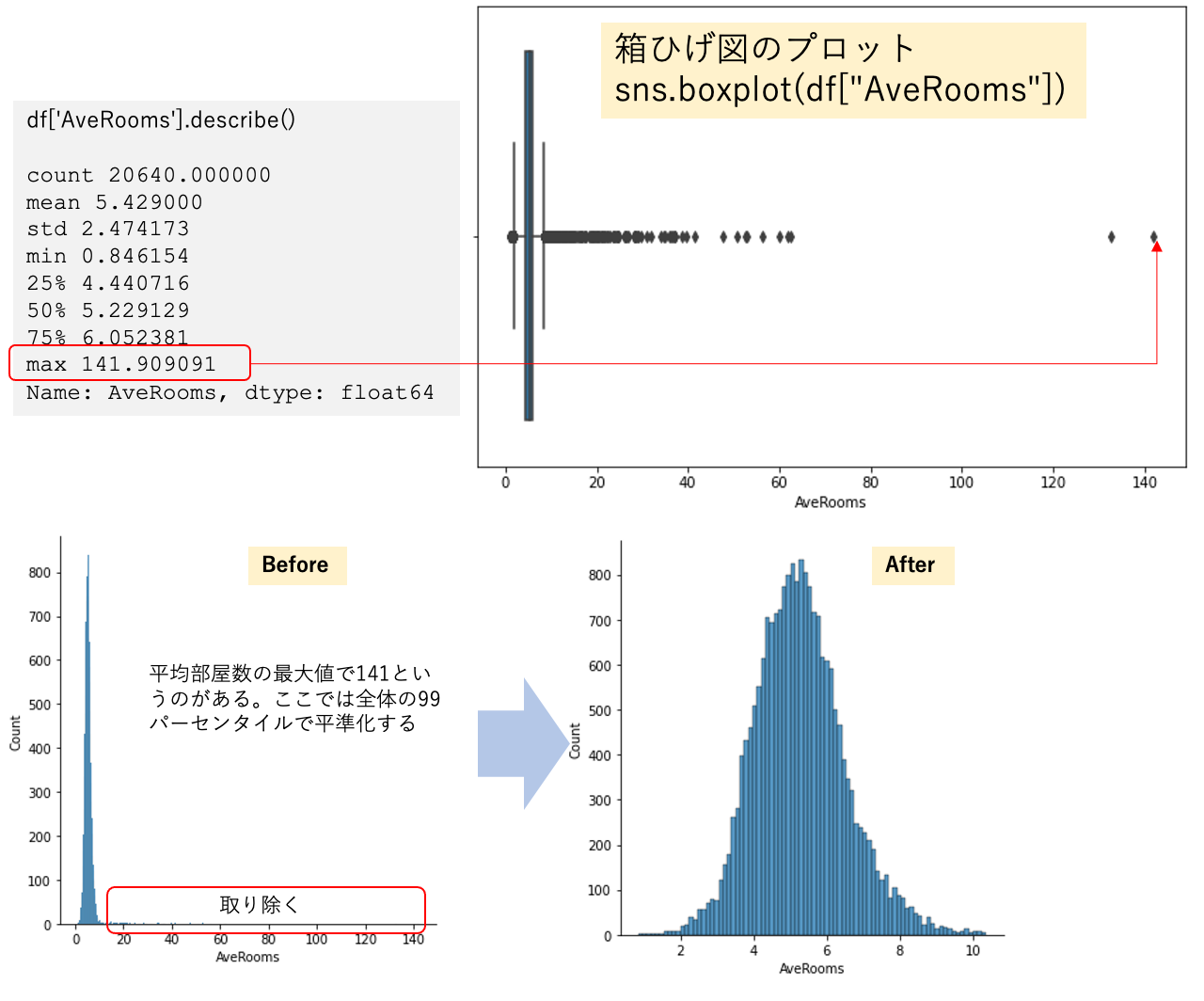
ドメイン知識による次元削減
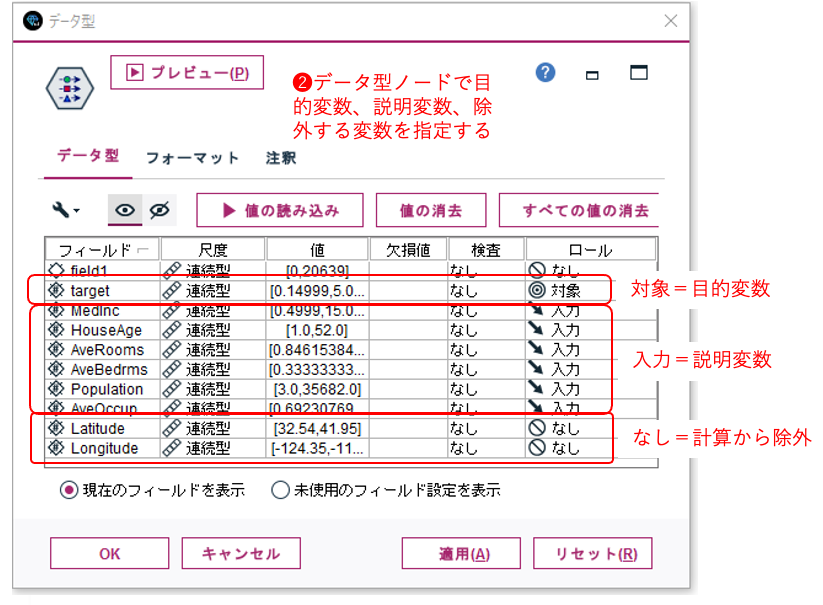
特徴量の抽出で重要なタスクはドメイン知識を持つ、データセット由来の業界知識・専門知識を持ついわゆる専門家からデータセットのカラムのうち、特徴量(説明変数)としては 適切で無いものを除外する事です。今回の不動産価格においてはその地理的座標は不要とのことなので、ブロックの地理的座標軸(経度:F6、緯度:F7)は除きます。
- 説明変数のうちドメイン知識よりブロックの地理的座標軸(経度:F6、緯度:F7)は除きます。
ドメイン知識で除かれる経度:F6、緯度:F7のデータの影響を可視化
経度:F6、緯度:F7を除く前のXGBoostによるFeature Imporanceの計算をPythonで行ない、経度:F6、緯度:F7の影響を見ておく事とします。 Code は以下の通りです。 とても簡単なコードですね。
from sklearn.datasets import fetch_california_housing
import pandas as pd
import seaborn as sns
import xgboost as xgb
import matplotlib.pyplot as plt
from pylab import rcParams
%matplotlib inline
rcParams['figure.figsize'] = 9,6
housing_array = fetch_california_housing()
x = housing_array.data
y = housing_array.target
xgb_model = xgb.XGBRegressor()
xgb_model.fit(x,y)特徴量を可視化します。左の図のとおり、経度:F6、緯度:F7は計算上は、住宅価格の決定要因としては、収入に次ぐ要因となっています。 それらを除外して再計算した結果を右側に並べて見るとその影響がよく分かります。
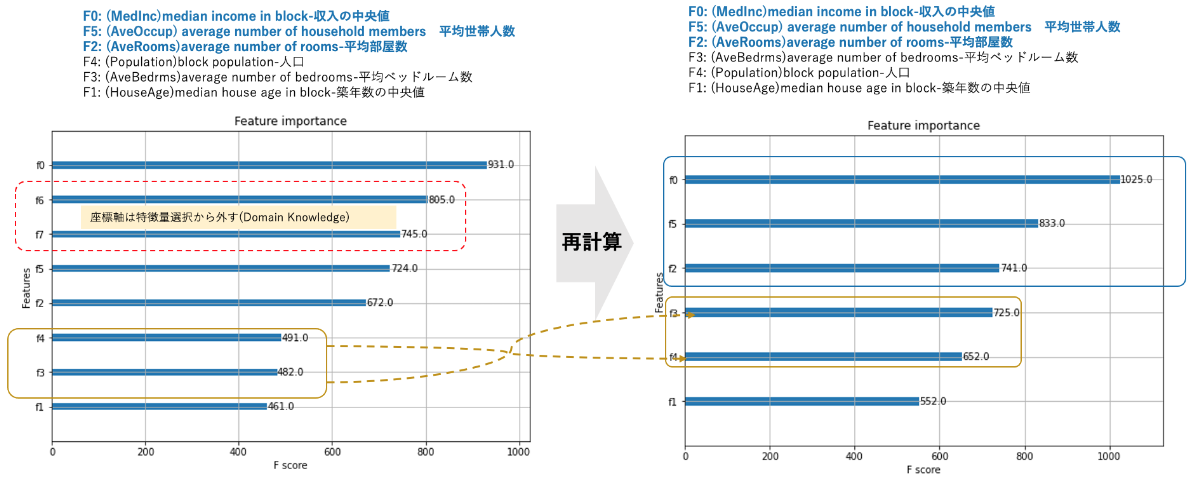
Python (Sciki-Learn) vs SPSS® Modeler 特徴量計算を比較する
次に同じデータセットでSPSS® Modeler を使って計算します。 左がPythonで右がSPSS® Modeler での計算結果です。 計算結果に少しだけ、差異があります。 Python では:
と平均住宅占有率が2番目に大きな影響力があるとい結果でしたが
SPSS® Modeler では:
とPython では3番目の平均部屋数が2番目という結果でしたが、それ以外は同じ順位でした。
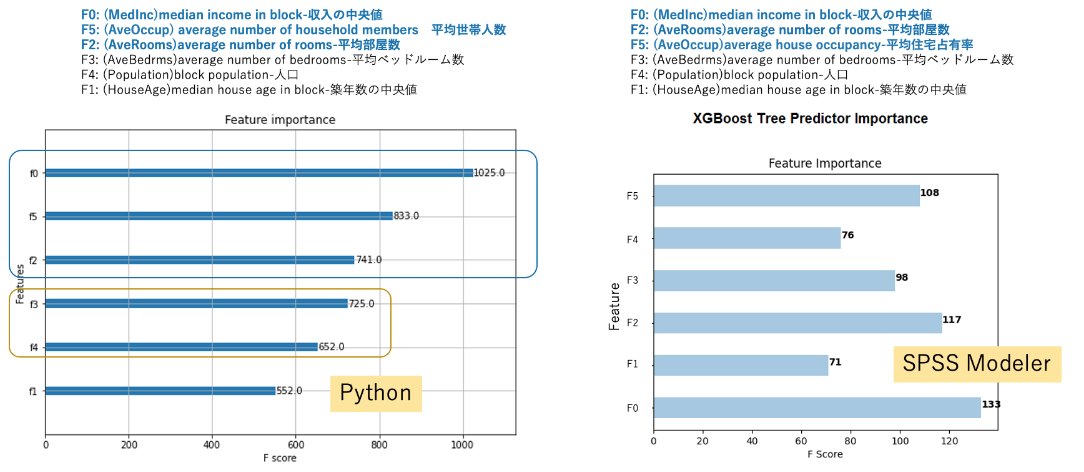
*SPSS® Modelerでは、Feature をF1から始めて作図されます。本ブログではPythonとの比較のため、Python と同じようにF0からに変更しています。
SPSS® Modeler ストリームと設定
SPSS® Modeler 上でのストリームと設定の概要は以下のとおりです。
ストリーム画面
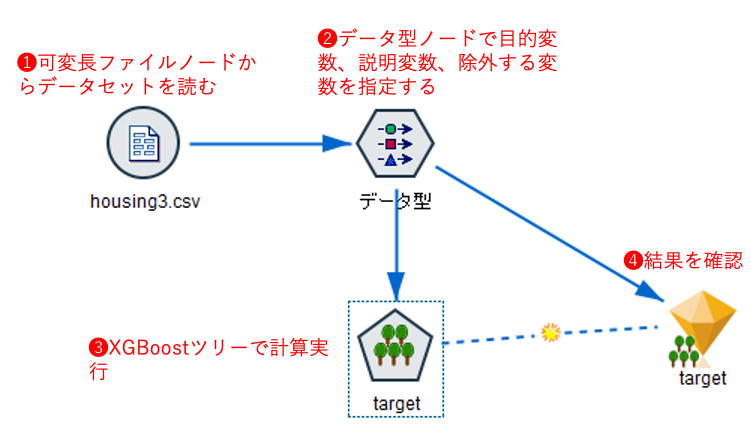
データ型ノードの設定
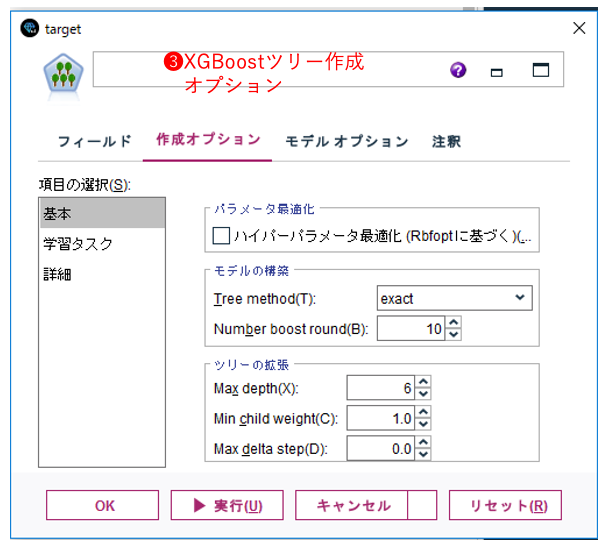
XGBoost Tree Pythonノードの作成オプション
- 収入(お金に余裕があるかどうか) > 部屋数(家の広さ)> 平均世帯人数(何人暮らしか)
- 築年数はさほど影響しない
- 計算に使用したアルゴリズム XGBoostにおいてPython, SPSS® ともほぼ同じ結論を導いている
