今回は、個々の説明変数が退職率へどの程度の影響を及ぼすか。すなわち、モデルの解釈(interpretability)としての「相関係数(coefficient)」の扱いについて説明します。 「ロジスティック回帰分析_その2」 では、各社員の退職の予想を二項ロジスティック回帰モデルにダミー変数を加えて的中率(hit ratio)をアップする手順を解説しました。 そのモデルを利用して説明します。
データ分析屋としては的中率(hit ratio)の最大化に進みたいところですが、クライアントの人事や現場は、むしろ何が退職率に影響しているのか、影響度の度合いについての検討を望んでいることが多いと感じます。
使うデータは、Kaggle よりHRデータ からダウンロードできます。
チートシート
| やりたいこと | 方法 |
|---|---|
各説明変数の相関係数(θ)の変数coefを得る |
coef = LogReg.coef_ |
| データフレームを転置する | df = df.T |
'LogReg : LogReg.fit(X_train, y_train)で学習(fit)済オブジェクト
今回使うデータのポイント
- 退職状況(attrition)に関する人事データ「ロジスティック回帰分析_その1」 で得たロジスティック回帰分析モデルの各説明変数の係数と説明変数の統計量を調べます
- 相関係数の正負、絶対値より予想に対する影響度(interpretability)を考えます
サンプルデータセットについての記事で紹介しているHRデータです。
サンプルオペレーション
以前の記事で紹介したデータフレーム同士の左結合および列名の変更を使って、データハンドリングをします。
変数LogRegは二項ロジスティックアルゴリズムliblinearで定義され、トレーニングデータで学習(fit)済です。相関係数は、coef_アトリビュートから得ることができます。
1
2
3
4
# 「ロジスティック回帰分析_その1」でfit済み
# LogReg = LogisticRegression(solver='liblinear')
# LogReg.fit(X_train, y_train)
print(LogReg.coef_)
[[ 3.64089914e-02 2.55992323e-02 -2.47726126e-01 -4.10522161e-01
-2.64106383e-01 -1.31124028e-04 9.08532467e-02 4.53165931e-01
-3.39360350e-02 -4.91441426e-01 -9.35272936e-02 -6.12707786e-02]]各説明変数の統計量はy_test.describe()で得ることができます。 ここでは、LogReg.coef_で得たcoefと統計量をそれぞれデータフレームにして結合します。結合に当たり、各々のデータフレームを転置(行と列を入れ替え)て 12 x 9 のデータフレームにしています。
また、最初に表示する数値を小数点以下1位までにして、大小関係を分かりやすくさせています。
1
2
3
4
5
6
7
8
9
10
11
12
13
# 各説明変数の相関係数(coef)を取得する
pd.options.display.float_format = '{:.1f}'.format
coef = LogReg.coef_
df_coef = pd.DataFrame(coef)
labels = df_test.columns
df_coef.columns = labels
df_coef = df_coef.T
df_coef = df_coef.rename(columns = { 0 : 'estimate'})
# 検証用(答え)のデータフレームの各説明変数の統計量を取得する
df_describe = df_test.describe()
df_describe = df_describe.T
df_coef_sum = pd.concat([df_coef, df_describe], axis =1)
df_coef_sum
結果は、以下のとおりです。
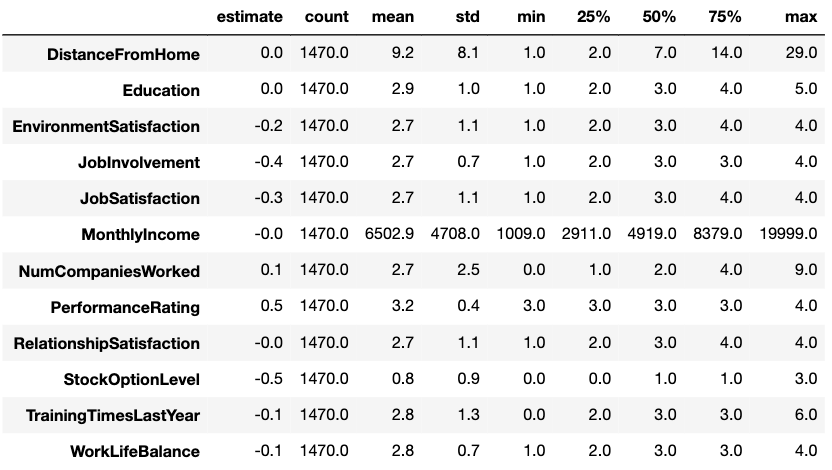
line by line で説明します。
各説明変数の相関係数(coef)を取得する
- 係数の正負、絶対値を分かりやすくするため、表示を小数点以下1位までにします
- 変数coefに相関係数を代入します
- df_coef としてコンストラクタでデータフレーム化します
- df_testの列名を変数lablesに格納します
- df_coefの列名をlabelsの内容に入れ替えます
- データフレームの行と列を入れ替え 1x12 を12x1 にします。インデックスがそれまでの列名に置き換わります
- df_coef の新しい列名を estimateとします。それまでは、インデックス番号0でした
検証用(答え)のデータフレームの各説明変数の統計量を取得する
- 検証用のデータフレーム(df_test)の統計量をdf_describeに格納します
- データフレームの行と列を入れ替えそ、 8x12を12x8にします
- df_coefと df_describeを左結合し、新しいデータフレーム df_coef_sum とします
- 表示させます
係数の影響度の考察
相関係数の絶対値が0.3を目安に正の相関=数値が大きいと1(退職)になる確率が大いと考えます。マイナスの場合はその反対に在職する確率が高いと考えると以下のようになります。
- 退職するに影響すると考えられる説明変数
- Peformance Rating 業績評価 0.5 (ただし、Ratingは3,4しかない)
- NumCompaniesWorked(転職回数) 0.1(やや影響あり)
- 在職するに影響すると考えられる説明変数
- StockOptionLevel ストックオプション -0.5
- JobInvolvement 職務環境 -0.4
- JobSatisfaction 職務満足度 -0.3
- EnvironmentSatisfaction 環境満足度 -0.2
- TrainingTimesLastYear 直近の教育機会 -0.1(やや影響あり)
- WorkLifeBalance ワークライフバランス -0.1(やや影響あり)
- ほとんど影響が見られない説明変数
- DistanceFromHome 通勤距離 0
- Education 教育分野 0
- MonthlyIncome 月収 -0
- RelationshipSatisfaction 対人関係満足度 -0
多重共線性でドロップした説明変数を忘れないこと
多重回帰もそうですが、ロジスティック回帰分析では説明変数間は独立性(相関が無い)が求められています。そのため、以下の説明変数は相互に相関があるとして モデル作成時にドロップしました。
- Age
- JobLevel
- PercentSalaryHike
- TotalWorkingYears
- YearsAtCompany
- YearsInCurrentRole
- YearsSinceLastPromotion
- YearsWithCurrManager
3のPercentSalaryHike(賃金上昇率)がPeformanceRating(業績評価)と相関でドロップしましたが、それ以外はMonthlyIncome(月収)との相関関係があったので、
ドロップしました。年功序列の傾向の強いデータですが、MonthlyIncomeの係数は-0となり、回帰分析の結果からはほとんど退職には影響していないということです。
すべての説明変数を使えないことは、なんとなく疑問が生じる部分かと思います。対案として、ドロップした説明変数と入れ替えるなりして、影響を見極める必要があります。
参照 sklearn.linear_model.LogisticRegression
ひとこと
多重共線性を考慮するため、いくつかの説明変数をドロップして回帰分析をしました。折角集めた説明変数が使われないことになり、ここは異論があるところだと思います。また、ここでは触れていませんが、相関係数 coefficient はその信頼性を担保するため、計算結果の確率、いわゆるp値が5%から1%以下が求められ、15%以上の確率で計算されるとなると、偶然性が排除されないので、ここでも折角収集した説明変数を使えなくなってしまいます。ここにそもそもデータ解析をする目的は、モデルの性能評価だけではなく、予測値からどうアクションして目標に達成するかというビジネス的な議論の方向性が見えてきます。 次回以降、この点も含めてブログで綴りたいと思います。